Rhythm

Before launching into a discussion of various aspects of rhythm, here are some pages dedicated to some of our most common specific practical rhythmical problems:

1. Dotted Rhythms
2.     Syncopations and Offbeats
3.     Tuplets, Exotic Rhythms and Crossrhythms

Of the three principal elements of the musical language – rhythm, melody, and harmony – rhythm is the most primal. But does “rhythm” belong in the musical language-and-interpretation department or in the technique department ?

Obviously, choosing a tempo, and then using tempo fluctuations as expressive devices falls into the category of interpretation. But deciphering (reading) notated rhythms correctly and quickly is a purely intellectual skill (“technique?”) which has nothing to do with musicality, interpretation or even playing the cello. It is possible to be, at the same time, a very good cellist and a very bad “rhythm-reader”. And it is likewise possible to be the opposite: a very good “rhythm-decipherer” but a very bad cellist. So even if we have read and understood the rhythms correctly, actually playing them correctly at the instrument (especially without rushing) depends very much on our physical skill (technique) at the cello. In conclusion,  rhythm – like sound, and pitch – is an absolutely fundamental, wide-ranging subject that straddles (falls into) every different category of musical and instrumental skills.

The most primitive music is purely rhythmic. Melody, harmony and beautiful sounds come later. The evolutionary path of music starts with rhythm, then adds tuned percussion and singing (melody), and finally adds harmony and counterpoint. The Australian aborigines had (and still have) a form of collective music-making that was purely percussive. In the Basque language – considered by linguists as a “living fossil”  – the word for “play music” (jo) is the same as the word for “hit”. In Africa, drumming was (and still is) one of the principal forms of traditional music-making. The more predominantly “rhythmic” the music is, the more primal it will be (a good example of this is the “Ritual Dance” from Stravinsky’s “Rite of Spring”).

In music all over the world, loud, driving, repetitive percussive rhythms seem to be associated with a direct communication line to our physical, primitive brain. In fact, they actually seem to switch off the higher levels of the brain! By contrast, melody and harmony seem to appeal to those higher levels of the brain. This difference can be seen, heard and felt beautifully by comparing the music of the Rolling Stones with that of the Beatles, and reaches its culmination in “death metal” where the frantic pulse never stops and doesn’t even ever slow down. This is African tribal drumming gone berserk!

1. THE ORIGIN OF RHYTHM

Where, outside of music, can we find regular pulsating rhythms such as those that occur in music? Are there any in the inanimate world?  The rhythms of the inanimate world seem to be either very slow (the seasons, night and day) or very irregular and disorganised (waves, wind, rain, the occasional tree fall or rockslide etc). Because of this, all of these rhythms are not musical in the traditional sense of the word (but they are used widely in a lot of contemporary classical music ).

It’s easy to associate regular, steady rhythms with the “mechanical world” of machines and metronomes. But in fact, the original source of organised, regular, pulsating rhythms is life and living beings (not of plants, but rather of the animal kingdom). Machines move in regular rhythms, but it is in life – animal and human – that we find the origin of regular “musical” rhythms which – unlike the rhythms of machines – fluctuate according to the emotions of the moment: heartbeat, breathing, movement (walking, dancing, running, skipping etc). Rhythm is life. At death (or, in the case of machines, mechanical breakdown) all of these movements stop.

RHYTHMICAL FREEDOM

As mentioned above, living rhythms are profoundly linked to emotions. Only in life (unlike in the world of machines), do all these regular rhythms respond dramatically to emotional states. And of course, emotions and music existed well before the invention of the first metronome, motor or sewing machine. The idea of an unwavering, absolutely strict tempo is perfectly unnatural outside of the mechanical world. We need to remember that the metronome was a German invention dating from 1815, so it’s not surprising that its greatest musical use in interpretation is in the works of Beethoven (1770-1827) perhaps more than with any other composer. Apart from that, the metronome is a phenomenally useful tool for practising rhythmic control, but a destructive demon when given total priority over performance and interpretative imagination.

We can divide rhythmic freedom into two overlapping categories, according to the type of music we are playing. “Rubato” refers to the freedoms we might take in music with singing, melodic character while “rhetoric” refers to the freedoms that we might use in more declamatory music.

But then there are those unfortunate involuntary, unconscious rhythmic freedoms that we take without being aware of them. There is a big difference between a problematic heart arrhythmia and a beautiful organically fluctuating pulse rate that is responding to changing emotions. In the heat of the moment our sense of time tends to compress with the result that our long notes and rests get shorter, and our fast notes get even faster (see “Rushing” below). In ensemble playing sometimes the group actually slows down as everyone is waiting for (accompanying) everybody else. This almost never happens in “solo” playing, which tends to suffer from the reverse phenomenon.

Both rubato and rhetoric are wonderful expressive tools but it is only after we are capable of playing a passage correctly in time and with an absolutely steady pulse that we should really allow ourselves to consciously decide to play around with its rhythm/pulse.

2. THE CONCEPT OF SPEED

Einstein said that his Theory of Relativity was largely inspired by music. This is not surprising. Not only are musical intervals totally relative, but concepts of speed, tempo and rhythmic values also. Let’s look now at these:

2.1 TEMPO (SPEED):

In outer space, astronauts are flying around at tens of thousands of kilometres per hour, but because there is no air friction (wind) up there, it feels to them as though they are not moving at all. The same phenomenon occurs when we travel by plane: we feel no rushing wind, we are making no effort, the plane is not vibrating and shaking like crazy (hopefully), the earth underneath us is moving very slowly …….  the whole experience is so smooth and easy that we don’t feel that we are moving fast at all.

So the concept of fast has two completely separate components: the objective and the subjective. The objective speed can be measured: in the case of music it would be the “notes per minute” (or any other time value). The subjective sensation of speed however could only be measured by physiological measurements that evaluate our physical and emotional state, because the feeling of speed, is usually just the feeling of difficulty, stress, sensory overload, loss of control. When we play something fast but effortlessly, it no longer feels fast. Trills and tremolos are good examples. Here we are playing up to 10 notes per second (720 per minute). This is fast, but, because it is not particularly difficult, it doesn’t feel “fast”. See Fast Playing for further discussion.

Yes, the concept of “speed” in music is certainly a bizarre one. Look for example at Haydn’s C major cello concerto: we could basically leave our metronome on 135 bpm (beats per minute) for all three movements. In the “Moderato” first movement it is the quaver (8th note) that moves at 134 bpm, in the Adagio movement it is the semiquaver (16th note), and in the “Allegro Molto” last movement it is the minim (half note). The change in the feeling of speed comes not from the speed (frequency) of the note changes, nor from any change in this underlying 134 bpm subdivision but rather from the speed of the fundamental musical pulse. This “fundamental speed” is what we dance to intuitively and is what makes us “know” if a piece is “fast” or “slow”, independently from the speed at which the notes are changing.

2.2 NOTATION AND SPEED: THE RELATIVITY OF RHYTHMIC NOTE VALUES:

Rhythmic note values do not indicate speed. Semiquavers in an Adagio can be slower than crotchets in a Presto. Put in another way, the exact same music, played at exactly the same speed, can be written as an Adagio, a Moderato, or a Presto simply by using the appropriate rhythmic note values. Frequent examples of this can be found in the orchestral repertoire, where the musician’s rhythmic decoding ability is tested to the limit. Look at the following example from the Overture to Verdi’s opera “Nabucco”:

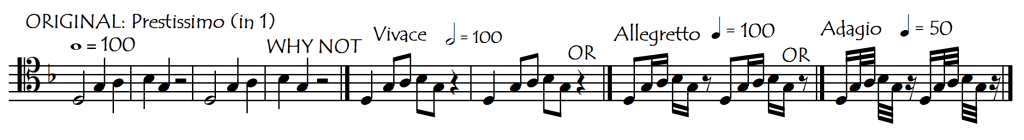
The cello repertoire also has some curiosities in this department. Normally a pulse of 120-140 beats per minute would be an approximate speed for an “Allegro”. In the first movements of Haydn’s two cello concertos however, this “Allegro = 120” pulse applies to the quavers (eighth notes) rather than, as we might normally expect, to the crotchets (quarter notes).

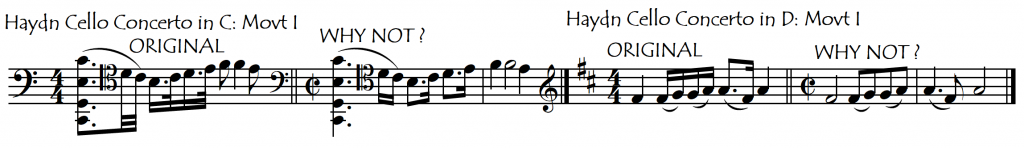
Like the Haydn cello concertos, the first movement of Bizet’s “Symphony in C” is also marked “Allegro” (Vivo) but here the quarter-note speed is approximately 360/minute compared to Haydn’s 70/minute making the quarter-note speed in the Bizet more than five times faster than in the two Haydn Cello Concerto “Allegros”! With this speed difference, one 4/4 bar of Bizet takes less time than one crotchet (quarter-note) of Haydn. Another, even more extreme example comes from the second movement of Shostakovitch’s 8th Quartet, which has the tempo marking “Allegro Molto: semibreve (whole-note) = 120”. This is the equivalent to 480 quarter-notes per minute (= 120 bars per minute) which is more than seven times faster than our Haydn cello concerto first movements!

In the above Shostakovitch example, the music looks “normal” until we notice the “abnormal” tempo marking, which makes this music go unexpectedly fast. In the Haydn examples the opposite is the case: the music “looks” fast (with its small note values) but is played slower than it looks. Perhaps the most extreme example of music that is played “slower than it looks” comes from Messaien’s “Quartet For The End Of Time”. In the fifth movement, marked “infinitely slow”, even though the music looks “normal” and is notated with a “normal” 3/4 time signature, the pulse is 44 semiquavers/minute. This means that four crotchets (quarter-notes) last approximately 22 seconds. Compare that to the Presto of Shostakovitch’s 8th quartet in which each bar of four crotchets lasts only half a second. In other words, in the time it takes to play four crotchets of Messaien, we will have played 176 (44 bars) of Shostakovitch!

Beethoven’s Eighth Symphony also provides us with two extreme cases: the “slow” second movement has a crotchet (1/4 note) speed of 44 per minute and uses many 64th notes (hemi-demi-semiquavers with four beams) while the Allegro Vivace Finale has a crotchet speed of 330 per minute and a smallest note value of an eighth note. This means that one quarter-note from the second movement lasts as long as two full bars of the last movement !! If this was a piece by Bach, we could think that the composer was playing a musical joke, in the sense that this is the Eighth Symphony and, with this notation, the speed of the finale is eight times faster than that of the second movement, but Beethoven did not have Bach’s sense of mathematical humour so any connection is probably just coincidence. If Beethoven had doubled every note value in his slow movement and halved every note value in his final movement then his notation would have been considerably easier to read, with the fastest notes of the second movement being now only 32nd notes, and the fourth movement using 16th notes as the fastest notes.

The repertoire abounds with such anomalies, which is why musicians need also to be mathematicians, experts in instantaneous subdivisions.

BACH’S RHYTHMIC NOTATION ANOMALIES

In some movements of the Bach Cello Suites (and Solo Violin Partitas and Sonatas), Bach also notates his music using “bizarre” note lengths (time signatures). In the Courante of the Fifth Suite and the Sarabande of the Sixth, he uses rhythmic values that would seem to be twice too long (see Bach: Rhythmic Factors). This is the way pre-Baroque composers usually notated their music (see Purcell, Ortiz, Dowland etc) but it is unclear why Bach did this only in these two isolated movements. And then he sometimes does the exact opposite, using – in very slow music – note values of half the “normal” length. The best examples of this from his unaccompanied string repertoire (as shown in the table below) are the Allemandes of both the Sixth Cello Suite and the first Solo Violin Partita, the Grave that starts the A minor Solo Violin Sonata, and the Adagio that starts the g minor Solo Violin Sonata (once again, see Bach: Rhythmic Factors).

This stuff is hard to read! We are just not used to reading such small note values. Bach loved mathematics and reading this is mathematically challenging for the normal musician. To decipher this music we don’t even need our instrument: this is a mathematical exercise for which we just sit down with the music and a pencil and try and figure out the rhythms. This level of reading complication is however perhaps unnecessary.

Counting 3 or 4 beams on a note is as difficult (if not more) than counting many ledger lines on very high or low notes. To avoid having to decipher the pitch of notes far above or below the stave, editors normally change the clef or use the “8ve” sign. But rewriting the rhythms in a more user-friendly way is not at all common. The only real usefulness of these tiny rhythmic values is to make it clear that the essential pulse of the music is very slow. If we write this music out using more readable note values (doubling the value of each note) we will have to be careful not to change Bach’s original idea. He obviously wrote it like he did in order that the piece would be felt (“danced”) with a very slow crotchet (1/4 note) pulse in which the short notes are simply light, fast-flowing, fioritura ornamentations (a characteristic of Baroque music, painting and architecture). Let’s play it like that, but let’s also make it readable without the need for a calculator or a magnifying glass! These movements of Bach are available on this website in both the “original” notation and the “easy to read” version (with longer note values).

The relationship between musical notation and musical speed is certainly an interesting one. See “Reading Problems” for more discussion of this theme.

2.3 RUSHING THE FAST BITS AND HOW TO AVOID IT

Emotivity is what gives us rubato and rhetoric. But in the heat of the moment, our sense of time tends to compress with the result that our long notes and rests get shorter, and our fast notes get even faster. “Mind the gap” would be a very good mantra for musicians because as time condenses with the intensity of the moment, so the gaps that we put between the notes also condense (shrink). This manifests especially in the asymmetries of dotted rhythms where the long note is almost universally shortened and the short note consequently comes too early.

It is an unfortunate fact of human nature that the faster we do things, the more impatient and accelerated we become. This is Newton’s First Law of Motion (also called the Law of Inertia) but also applicable to psychology. Whereas mechanical objects tend to slow down under the effect of friction, the mind has no friction so once it starts accelerating it becomes – unless we consciously put the brakes on – like a rocket hurtling through space with nothing to slow it down. A vehicle without brakes is like a musician without a metronome because, for most musicians, the vast majority of the time the metronome is telling us that we are ahead of the beat rather than behind the beat.

Another unfortunate fact of human nature is that when we are in a state of “stress” we tend to do things too fast. The musical manifestation of this “natural psychological law” is that we tend to rush the most, difficult, complex, musical passages (these are the ones we call “fast”) which are also, sadly, those that we can least afford to rush. When we think, “this passage has to go fast”, we can very easily find ourselves automatically thinking also that:

• it has to go as fast as possible
• it has to feel difficult

These are however two very natural (but highly destructive) thinking traps, into which we can so easily fall in fast passages. Here we are measuring the speed subjectively, confusing speed with difficulty. This is the panic response.

When we play a fast passage “a tempo” (at speed) it is helpful to think the absolute opposite. Instead of thinking “play it as fast as possible” and “this is difficult” we need to think “play it as slow and easy as possible”. Here is where the metronome can be our mental brakes, teacher, saviour and guardian angel. The metronome is purely objective, and it is amazing how slowly it actually goes in the fastest, trickiest passages. It’s a good idea to practice our fast-playing not just “in time” with the metronome, but even sometimes a tiny bit behind it, in order to get used not only to not rushing, but also to playing as slowly as possible without actually being left behind by the metronome. In this way we are testing the lower limit of the fastest passages – “how slow can I play this passage without getting behind the metronome?” –  rather than always testing the upper limit (the speed at which we crash). When under stress it is almost always more important (as well as more difficult) to be lazy, languid and half-asleep than it is to be intense, on-the-ball and hyper-alert.

The subject of “rushing” is looked at in greater detail on its own dedicated page:

Rushing

WHAT IS “TOO FAST” ?

“Too fast” can have two definitions, one of which is physiological and the other, musical. Musically speaking “too fast” is when we are ahead of the metronome or of our musical colleagues. Physiologically speaking “too fast” is the speed above which we start to lose control and accidents start to happen.

3: BINARY OR TERNARY: WHAT’S THE DIFFERENCE?

The most basic building block of musical construction is the individual note, but these notes are most often organised rhythmically into groups of either twos (binary) or threes (ternary). In “binary” music the basic rhythmic units are in multiples of 2 while “ternary” music uses groups of three. Some music is simultaneously binary and ternary: in 6/8 and 12/8 time signatures for example the fundamental triplet units are grouped in pairs whereas 9/8 music is pure pedigree ternary.

It is curious how one simple group of 2 or 3 notes can seem to have parallels to fundamental concepts in life, nature and philosophy. Are there any living creatures with three legs, wings or arms? Even internally, we have two kidneys, ovaries, testicles, chambers of the heart lungs and brain – but do we have three of anything”? So much of the world (not just music) is composed of binary systems in which, by definition, the fundamental unit of construction is “the couple”. The couple can be composed of identical twins, perfectly matched opposites (yes/no, 0/1, Yin/Yang, +/-, attraction/repulsion, male/female, tension/release etc.) or everything in between, but they go together, stay together and form a complete, balanced, unity. The simplest structures are usually binary. Is it any wonder that the pyramids and a successful menage-à-trois (threesome) are considered to be extraordinary achievements!

Adding an element to convert binary into ternary involves adding instability. Now, instead of just two opposite options, there is a third “midway” option. Instead of just “yes” and “no”, now we have “yes”, “no” and ……… “maybe”. In musical terms, this means that instead of marching inexorably forwards, we now introduce a sideways step and the music can start to dance, wander, wonder and turn around on itself. This is dangerous stuff, and this is why most military music uses binary key signatures (think of military marches for example). At the opposite extreme, we have the waltz – that most charming, graceful and sensuous form (Tchaikovsky’s favourite) – which uses 3/4. In the ultimate fascist state, music in 3/8, 3/4 and 9/8 would be banned, while 6/8 and 12/8 would be regarded with suspicion!

The use of ternary rhythms takes us into a somewhat more flowing, artistic, more asymmetrical, less mechanical world, in which there is more time for relaxing. Now, for each strong beat, there are two beats to relax on. This resembles more the rhythm of (relaxed) human breathing, in which we normally take longer to expire (relax) than we do to inspire.

When each pulse of these mini-groups (of two or three notes) has a newly articulated note on its beginning, then the group is perfectly balanced, symmetrical, stable, “complete”……  but that can make them rhythmically somewhat predictable (boring). Adding a third beat to the binary couple opens up new geometrical (rhythmic) possibilities, but prolonging a note over the next beat (by putting a dot on it) takes us even further along this path to freedom, asymmetry, instability, humanity, dance  ….. and interest. This leads us into the new and wonderful world of syncopations and dotted rhythms that culminates in the laid back world of jazz, bossa nova, pop etc in which a huge proportion of the new notes actually start between the beats (see Fascism in Music).