Tuplets, Bizarre Barlines, Exotic Time-Signatures and Crossrhythms
In this article, we will talk about some of the more irregular, complex elements of rhythm that we will come across in our musical journeys. We will order these elements in a list that follows an approximate pedagogical hierarchy of increasing complexity:
- tuplets
- irregular time signatures
- cross-rhythms
- irregular phrasing
THE HISTORY AND GEOGRAPHY OF BIZARRE RHYTHMS
Apart from the tuplets, a great amount of the rhythms that we will be talking about on this page come either from 20th-century music or from non-western-European traditional music. Normally, traditional Middle Eastern, Indian and Asian music does not march to the same regular pulses that most western musicians are accustomed to, and as we travel east and south from western Europe the local rhythms become more and more “bizarre” to western ears.
The same phenomenon occurs as we travel (both ways) through time. Starting in the four-square “Classical Period” and going forward in time, the likelihood of encountering bizarre and complex rhythms becomes gradually greater, culminating in 20th-century classical music where it often feels as if we have suddenly been blasted onto a totally different (rhythmical) planet. But also as we go back in time we are eventually confronted with some bizarre rhythmic notations because in “Early Music” the notation rules and customs, notably concerning time signatures and the use of barlines, were still evolving (see also Bach: Rhythmic Factors).
NOTATION CHOICES: MAKE IT HARD OR MAKE IT EASY?
Any rhythm can be made to look hard if it is notated in a non-user-friendly way. Likewise, even difficult, complex rhythms can be made easier, at least to read, if they are notated in the most user-friendly way. It is useful to distinguish between the problems created by genuinely complex rhythms and those created simply by “bad” or confusing (deliberately or not) notation. Some composers seem to be more interested in showing how clever they are rather than in making the player’s task easier. At other times the question is “for which player should the notation be user-friendly?” In the following example, the second notation version is slightly harder for the top voice but hugely easier for the bottom voice.

The problems that are associated with sub-optimal notation are dealt with on their own dedicated page:
Rhythmic Notation Reading Problems
Let’s look now at some genuinely “bizarre” rhythms:
1: TUPLETS
The word “tuplet” usually refers to an irregular number of notes that are squeezed into one pulse, beat, or bar (measure). With “triplets”, we squeeze three notes into a space that would normally have two, with “quadruplets” we squeeze four notes where normally there would be three and so it goes on for quintuplets, sextuplets, septuplets etc. We can consider tuplets normally as a “special occasion” phenomenon, occurring individually (or often) in a piece but with no permanent “distorting” effect on the time signature or pulse. Tuplets are the easiest of the “bizarre rhythms”. We can practice them by playing scales and arpeggios with different numbers of notes in each beat: 3, 4, 5, 6, 7, 8, 9, etc. Major and minor scales are great for “sevens” because there are seven notes in each octave (see below).
QUINTUPLETS IN TURNS
One of the most common but most unsuspected uses of quintuplets is in turns. The use of the quintuplet can often be the secret trick that makes our turns sound improvised, expressive and graceful rather than mathematical and mechanical. Most commonly, for a quintuplet turn, the first note of our quintuplet is tied to the beat before:

At other times it might be the last note of the quintuplet turn that is tied to the following beat, or even perhaps both the first and last notes of the quintuplet turn that are tied over:

TIED TUPLETS = TANGLES
Ties (when the same pitch is slurred across a beat) create syncopations, which are looked at on their own dedicated page (click on the highlighted link). When ties and tuplets combine, we are often faced with some quite complex, sophisticated rhythms which require a highly developed rhythmical and/or mathematical sense – and lots of concentration – to both decipher and assimilate (play):

2: IRREGULAR TIME SIGNATURES
BINARY, TERNARY AND PRIME NUMBERS
The most basic building block of musical construction is the individual note, but these notes are most often organised rhythmically into groups of either twos (binary: 2/4, 4/4, 2/2 etc) or threes (ternary: 3/8, 3/4, 9/8, 3/2 etc). Some music is simultaneously binary and ternary: in 6/8 and 12/8 time signatures for example the fundamental triplet units are grouped in pairs whereas 9/8 music is pure pedigree ternary.
Prime numbers are those that cannot be divided evenly by any other (whole) number and prime numbers figure greatly in our bizarre rhythms section. The number “three” is the first (lowest) prime number and serves as our simplest introduction to the world of “irregular” rhythms.
Adding an element to convert binary into ternary involves adding instability. Now, instead of just two opposite options, there is a third “midway” option. Instead of just “yes” and “no”, now we have “yes”, “no” and ……… “maybe”. In musical terms, this means that instead of marching inexorably forwards, we now introduce a sideways step and the music can start to dance, wander, wonder, and turn around on itself. This is dangerous stuff for a military mentality, which is why most military music uses binary key signatures (think of military marches for example). At the opposite extreme from the military march-to-war, we have the waltz – that most charming, graceful and sensuous form (Tchaikovsky’s favourite) – which uses 3/4 or 3/8. In the ultimate fascist state, music in 3/8, 3/4 and 9/8 would be banned, while 6/8 and 12/8 would be regarded with suspicion!
The use of ternary rhythms takes us into a somewhat more flowing, artistic, more asymmetrical, less mechanical world, in which there is more time for relaxing. Now, for each strong beat, there are two beats to relax on. This resembles more the rhythm of (relaxed) human breathing, in which we normally take longer to expire (relax) than we do to inspire. Its non-binary nature gives ternary music a very interesting, lilting character that opens up huge avenues of expressivity, agogic accents and rubato.
TAKE FIVE
The next prime number after 3 is 5. Now we are really getting into interesting territory. We are used to the pentatonic scale and reading from a five-line stave, but we are not used to playing pentagramic (five-sided) music. Probably the first step to getting comfortable with fives is to play scales and arpeggios in quintuplets, fitting five notes firstly into each (slow) pulse of the metronome, and then fitting the five across two pulses. Whereas music that has five pulses per bar often incorporates an internal subdivision in which those five “beats” are subdivided into smaller groups (3+2, 2+3 or 1+2+2), this is not normally the case for quintuplets.
Playing music that is actually written with five beats to the bar (most commonly 5/16, 5/8 or 5/4) poses quite different problems to playing quintuplets. Most often, a bar of five pulses will incorporate an internal subdivision in which those five “beats” are subdivided into smaller groups, either 2 + 3 or 3 + 2. This sub-grouping may or may not remain identical during the entire piece/passage and we will certainly need to be aware of it in order to understand, play and follow the rhythm correctly. And even if the music is notated always with the same sub-groupings, conductors often decide to conduct certain bars with the opposite grouping, which can make our reading quite difficult.
I can think of no better way to introduce the concept of “music in fives” than by playing the jazz classic “Take Five”, for which the sheet music of a cello transcription is offered here below with its play-along accompaniment. This piece features the 3 + 2 subgrouping.
The second movement of Tchaikovsky’s Sixth Symphony is also in five and what’s more, it is the cellos who play its principal opening theme. It favours the 2 + 3 subgrouping but plays around with ambiguity: sometimes the melodic line (especially the slurring) of the cello part looks like 3 + 2:

We can download the cello part from imslp.org and play the entire movement with any recording.
Another fun example for getting used to music in fives is the Mission Impossible theme. Curiously, the Hollywood big-budget feature film version uses a dumbed-down 4/4 version of the theme but the original TV version is in 5 and uses consistently the 3 + 2 subgrouping:
Mission Impossible: CELLO PART
This cello part can be played along with the full orchestral version:
SUBDIVISION INTO FIVES: GINA LOLLOBRIGIDA
In “Take Five”, for example, the subdivision is always 3 +2 but in other pieces it might be something different. The Italian actress Gina Lollobrigida is currently 94 years old and her name is very useful in the bizarre rhythm department: Saying LOllo BRIgida is quite an attractive way to get comfortable with groups of five, and if we add the GIna at the beginning then we are ready for groups of seven. But while LOllo BRIgida works perfectly for quintuplets and 2+3 sub-groupings she’s no help at all for the “Take Five” grouping of 3+2, for which we will have to find another 5-syllable catchy expression that has the accent on the fourth syllable.
THE BASQUE FIVE
The Basques have a very curious and attractive dance called the “Zortziko”. The Basque word “Zortzi” means eight, but this dance is in five (well yes, five eighth-notes), and what makes it especially interesting is that the subgrouping of the five is 1+2+2, with an accent on the second of the five pulses that is as strong as the accent on the first pulse of each bar. Curiously, when the Basques play these dances, they usually convert them to a more comfortable, symmetrical 3/4:

Even Pablo de Sarasate, who spent much of his life in and near to the Basque Country, notated his Caprice Basque in 3/4 even though it definitely seems to have this Zortziko rhythmic structure. One can only wonder whether he notated it in 3/4 because he thought it would be too “shocking” to notate it in 5/8, or because he knew it was likely to be played in 3/4 no matter how he notated it …….. or simply because he was so used to hearing the Zortzikos being played in 3/4 !!??
It is curious that Ravel, also with Basque roots, uses the 5/8 rhythm as a major component of the last movement of his string quartet, but not with the Zortziko rhythm.
TAKE SEVEN
With sevens, Gina Lollabrigida comes into her own and can be used in her entirety, but only for septuplets that have a 2+2+3 subgrouping (or no subgrouping). Major and minor scales have seven notes in each octave so we can easily use them to practice our sevens. The following link opens up some scalic practice material that keeps always the seven notes of each octave in the same bar:
For any tuplet grouping or complex rhythmic pattern, finding catchy words or phrases with a matching number of syllables can be quite amusing as well as helpful (but may require a bit of censorship for the most colourful sayings).
3: CROSSHYTHMS
In this section we will look at music in which a stable underlying ostinato of short notes (for example 8th or 16th notes) is subjected to variations in the pulse (time signature) above it. Words can make this concept appear complex but musical examples make it very clear. In the following example, the eighth note speed never changes:

In the above example the underlying 6-note rhythmical ostinato figure is divided into either two groups of three notes or three groups of two. Especially at faster (dancing) speeds, this interplay between 6/8 and 3/4 gives a very attractive rhythmical effect and it is used a lot in Spanish and South American music. But here we are playing with small numbers (two and three) and therefore this is one of the simplest and most easy-to-feel crossrhythms. The world of crossrhythms rapidly becomes more of a mathematical juggling act as the numbers get bigger.
MENTAL GYMNASTICS AND MATHEMATICAL DIZZINESS: 12 = 4 x 3 = 3 x 4. THREES AGAINST FOURS
In the previous crossrhythm the fun comes from the fact that the number “six” can be divided into two groups of three or three groups of two. This is like juggling with two balls – not very difficult at all. Things get more complicated as our numbers get bigger. Look at the following examples in which we now divide bars of 12 notes into either four groups of three or three groups of four.
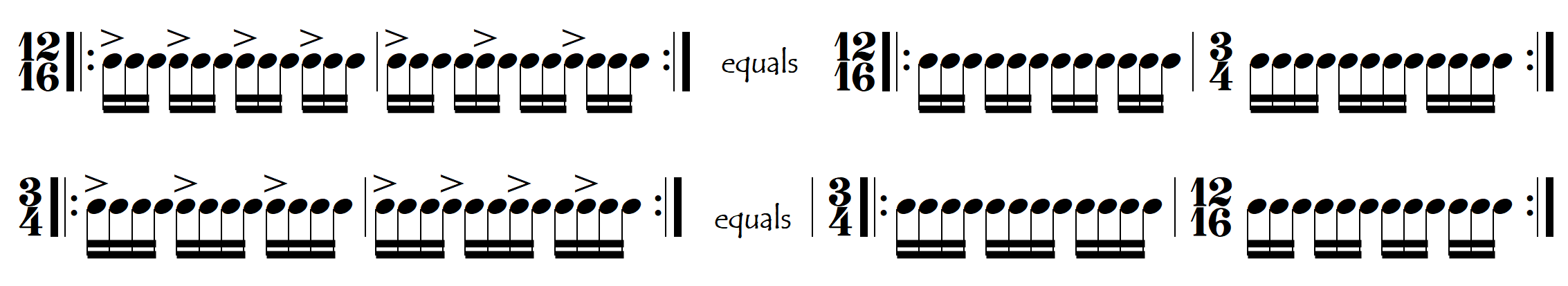
Now we are juggling with three balls. The following link opens some pages of exercises with which we can give our brain a workout in playing various configurations of these “three-against-four” crossrhythms:
Crossrhythms: 3 Against 4: EXERCISES
4: IRREGULAR PHRASE LENGTHS:
Bizarre, irregular phrase lengths take us into a larger-scale world of bizarre rhythms. Here it is not the bars or rhythmical figures that are of irregular lengths and proportions, but the phrases. See Phrasing
****************************************************************
WHAT IS THE SIGNIFICANCE (IF ANY) OF “BIZARRE ” AND IRREGULAR RHYTHMS ?
Does a lack of four-square symmetry reflect in any way some deeper characteristics of its creators ? Of their philosophy, approach to life, ways of thinking, use of logic etc ? Are “they” more in an artistic “dreamtime” of free association, improvisation, nature, curves? And are we “westerners” more in a “marchtime” of mechanics, structure, logic, clocks, numbers, metronomes, symmetry, right-angles and straight lines etc ? Is one “better” than the other ? What can we learn from each other ?
Responding to the last question, in the late 1950s, Dave Brubeck and his (jazz) quartet went on a trip to India and the Middle East with the goal of listening to the traditional music of these areas. Fruit of this voyage of discovery was the album “Time Out” (1959), dedicated entirely to pieces of their own original composition, all of which used bizarre, non-standard time signatures/rhythms. Although their recording company thought that this project was of little commercial interest, this record was hugely popular and was the first jazz album to sell more than a million copies!
It is curious that it has been principally western societies, powered by our “marchtime”, that have been the motors of the philosophical and industrial revolution since (more or less) the Renaissance period, that has ultimately achieved not only huge technological progress but also the submission (and destruction) of a large part of the natural world. Does “marchtime” have any sinister side effects? There is a huge subject of reflection here!
